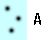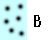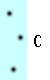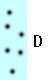Understanding Equations

| Multimedia | Practice Homework | Homework |

Context

We are all familiar with equations. When 2x=6 we know that x must be equal to 3. But in physical science equations are more that just relationships among numbers.

What is an equation in physical science?

In physical science equations show relationships among variables of a physical situation. Each symbol represents something physical. In physical science equations describe the physical world. They are a short-cut way of describing the world around us.

Explanation

In science equations don't just appear. They aren't dreamed up by a college professor to torment students. They are tools that help us better understand the world around us. They come from observations of the natural world. They model the physical world.

This section will help you:

• See how equations come about in science.
• Understand how equations can describe the physical world.
• Better interpret what an equation tells us.
• Be able to write equations from observations and data.

Model

Consider density as an illustrative example. Most people have some opinion as to what density is, but what does it really mean? A more detailed analysis of density will be done in a different course, but a short version will suffice for our purposes here.

What makes something more or less dense? Think of the dots in the blue boxes below as gas particles moving around in a container. How would you list A-D below from highest to lowest density?

Most of us think that the more compact something is, the more dense it is. Which of the particles are most compact? Which are least compact? Why?

Visually it looks like B is the most compact and C is the least compact. That would translate into B being the most dense and C being the least dense.

A and D seem to be somewhere in between, but how are they compared with each other?

Before we tackle that question, let's consider the difference between A and C. There are the same number of particles in each, but C is twice as large as A and so the particles in C have twice as much room to move around, making C less compact and less dense. Saying it the other way around: they both have the same number of particles, but A has less space for them to move around and so the particles in A are more compact and thus more dense. Keeping the number of particles the same and decreasing the amount of space for them to move around in results in a more compact situation and a higher density. These same statements hold true for B and D.

Now back to A and D. D has twice as many particles as A, but it also has twice the amount of space to move around in. Did the compactness change? It might depend on how someone defines compactness. How should we define it? How about the number of particles in a given space? If the amount of space in A (or B, since it is the same) is our reference space, we can say that the amount of space in A has a value of one reference space. In A there would be three particles for every reference space. In D there would be six particles for every two reference spaces (because B is twice as big as A). Three divided by one (A) is the same as six divided by two (D). From this definition A and D would have the same density.

As a check let's consider A and B. Remember we think B is more dense than A. In A there would be three particles for every reference space. In B there would be six particles for every reference space. Three divided by one (A) is smaller than six divided by one (B), and so A is less dense than B (or B is more dense than A).

Would you now agree that the following statements are always true when talking about density?

• If the number of particles stays the same, but the amount of space increases, then the density will decrease.
• If the amount of space stays the same, but the number of particles increases, then the density will increase.

Scientists are lazy and always want to say things in the most concise manner possible. Instead of saying "the amount of space" we define "volume" as the amount of space that something takes up and substitute volume for the amount of space. The number of particles can be directly correlated to the amount of material that is present. The amount of material present is the mass that is present. So, we can substitute "mass" for "the number of particles" in our statements.

• If the mass stays the same, but the volume increases, then the density will decrease.
• If the volume stays the same, but the mass increases, then the density will increase.

Do you agree that these are equivalent to the former statements?

Here they are using the word "constant" for "stays the same" in the statements and rearranging some of the phrases.

• For a constant mass, the density will decrease as the volume increases.
• For a constant volume, the density will increase as the mass increases.

Notice how it is getting shorter, but saying exactly the same thing each time.

To get it shorter we will have to make some more definitions. In math there are two concepts that are helpful here. They are directly and inversely proportional. If two things are directly proportional, when one increases the other also increases. When two things are inversely proportional, when one increases the other decreases. There is a bit more to it, but for our purposes this will do. Rewriting our statements using these definitions gives:

• For a constant mass, the density is inversely proportional to the volume.
• For a constant volume, the density is directly proportional to the mass.

To make it shorter now we will have to start using letters or symbols for words or phrases. We could, for instance, use a d to represent density and a V to represent volume. There is also a symbol that means "proportional to": ∝. The only other thing to designate is directly and inversely. Directly will be designated by simply writing the symbol, inversely will be designated by writing one over the symbol (e.g. 1/V). The statements can now be written:

• d ∝ 1/V (this means density is inversely proportional to the volume)
• d ∝ m (this means density is direcly proportional to the mass)

These are very concise ways of saying the same thing that we said in the beginning. Notice that they are a direct result of our observations. These statements express our understanding of density. They model density just like the sentences modeled density when we first started writing sentences to document the observations that we made.

In math, when one thing is proportional to two other things, you can combine the proportionalities. In our case this results in the following expression:

• d ∝ m/V (this means density is directly proportional to the mass and inversely proportional to the volume)

Notice that this one expression incorporates both of the previous expressions into it and means exactly the same thing. Proportionalities give the correct relationship between the various factors, but they don't allow us to calculate anything. In order to be able to calculate the density we need to transform the expression from proportional to equal.

Replacing the proportional sign with an equal sign requires a proportionality constant. The problem is that we don't know if the change in density is one to one with the change in mass (or volume). The density could change by two when the mass only changes by one and still be directly proportional. Or three changes in mass could only result in one change in density. Mathematically anything is possible in this regard.

We, however, are trying to model the real world density. Our expression needs to be consistent with our observations and experiments. The only way to determine what the proportionality constant must be is to do experiments. There is only one proportionality constant that will agree with experiment. In this case the experiments find that the proportionality constant is one. We can use this to write the following equation:

• d = (1)(m/V) (this means density equals one times mass divided by volume)

The number one is usually not shown in equations and so the final result is:

• d = m/V (this means density equals mass divided by volume)

The last equation incorporates all of the information that we know about density. It is a result of our analysis of physical observations. It describes the world around us for objects that have mass and volume. It is a model that we can use over and over again in different situations. Notice that it isn't an arbitrary relationship, but that it is specific to our understanding of density. It wasn't just dreamed up, it was derived from our explanation of observations from the physical world around us.

Thinking Questions

1. Is there more than one equation for density?
2. Do all equations in science have physical meaning?
3. How many variables have to be know in order to solve for an unknown?