Name
PHY107
What is the Boiling Point of Water on a Normal Day?
Exploration Phase
The Launch: As a Boy Scout and as a Scout leader I had opportunities to go camping in the mountains. I noticed that the potatoes wouldn't ever get done when boiled in water on top of the mountain. The water was boiling fine, but the potatoes never cooked. I learned to wrap them in foil and bake them in the fire.
From time to time I did some exploration to see if I could understand it better. I noticed that my Mom would always boil the potatoes vigorously with high heat. Sometimes she would put a lid on the pan and she thought it made the potatoes cook faster. Sometimes she added salt, but I always thought that was for taste. Maybe it made a difference in the cooking time as well?
As an initial exploration the temperature of water was monitored as it heated on top of a hotplate. The following data was obtained in five minute intervals:
| Time (min) | Temperature (oC) |
|---|---|
| 5 | 22 |
| 10 | 28 |
| 15 | 58 |
| 20 | 78 |
| 25 | 99 |
| 30 | 101 |
| 35 | 101 |
| 40 | 101 |
| 45 | 101 |
| 50 | 101 |
| 55 | 101 |
| 60 | 101 |
It was interesting that initially there were some bubbles, but they went away quickly. In the beginning the temperature went up as expected, but it stayed at 101 oC even though the hot plate was still on and providing heat.
Here are some questions that could come from the exploration.
- What were the initial bubbles that were observed?
- Why doesn't the temperature continue to go up?
- Is the boiling point of water usually 101 °C?
- What is the boiling point of water on a normal day?
- What is in the bubble when water boils?
- Does adding something (salt) make the water boil at a higher temperature?
- Does putting the lid on a pan make the water boil at a higher temperature?
- Does adding something or putting the lid on the pan make it boil faster?
- Does the temperature that water boils at change from day to day?
- Why does the water boil at a lower temperature on top of a mountain?
- What happens to the energy that is going into the water from the hotplate when the temperature isn't going up?
For this investigation the question "What is the boiling point of water on a normal day?" was chosen.
Experimentation and Data Collection
The objective of the experiment was to determine the boiling point of water for a normal day.
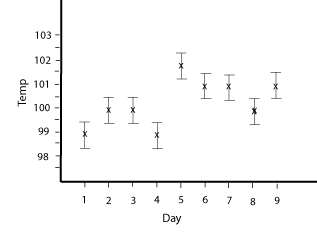
Since the conditions change from day to day it was decided that an average boiling point over several random, nonconsecutive days would be determined as the boiling point on a "normal" day. Water was brought to a boil on nine different days and the temperature of the boiling water was determined using a thermometer. The data can be averaged and an uncertainty in the data can be calculated. The average ± range/2 will be the boiling point for a normal day.
|
|
Making Sense
The average boiling point was 100.222 oC. The range was 3.0 oC. The result of the experiment is average ± range/2. Initially that is 100.222 ± 1.5 oC, or with proper rounding it would be 100 ± 2 oC.
Result: The boiling point on a normal day is 100 ± 2 oC.
Looking at the graphical data with error bars it seems that there may be a significant difference between some of the data. The error bars for the lowest value, for instance, don't come close to overlapping the error bars for the highest value. It looks like the boiling point can change from day to day. In a General Chemistry book the normal boiling point of water is given as 100 oC at 1.0 atm pressure. The condition of 1.0 atm pressure sounds like a clue. A pressure of 1.0 atm is "normal" around sea level, but if you are on top of a mountain the pressure could be much less. Maybe this is why the water boils at a lower temperature on the mountains? Given this, a variation in pressure due to weather conditions could be responsible for the different boiling points. There is no data about the weather conditions on the days that the boiling points were taken, but from general experience the pressure doesn't seem to change that much from day to day. An extension of the investigation would be to also collect pressure data and look at the boiling point on days when the pressure was a certain value, say 0.9 atm, 1.0 atm, 1.1 atm, etc.
A prediction from our data is that the average boiling point of water would be about 100° if it was found over a very large number of days.
A well-established equation* is available that allows calculation of the boiling point temperature from the pressure. Using that equation the following boiling point temperatures were calculated for the indicated pressures.
| Pressure | Boiling Point Temperature |
|---|---|
| 0.90 atm | 97.0 oC |
| 0.95 atm | 98.5 oC |
| 1.00 atm | 100.0 oC |
| 1.05 atm | 101.4 oC |
| 1.10 atm | 102.7 oC |
These calculations suggest that a small change in pressure, like we might expect from day to day, can change the boiling point by a couple of degrees, which could explain the variation in the boiling point data being reported in this investigation. This could be a major contributor to the uncertainty in the data and could explain the amount of uncertainty that is observed.
The experiment could be improved by controlling the conditions better, possibly including the time of day and the weather conditions. Focusing the question or better defining a "normal" day could result in a more satisfying answer. New questions from this investigation could be:
- How much does the atmospheric pressure vary from day to day?
- Are there other factors beside pressure that influence the boiling point?
- Is the change in boiling point linear with the pressure?
- Does the time of day make a difference in the boiling point?
- Does it matter if it is sunny or raining?
* The equation for calculating temperature (T) from pressure (P) is called the Clausius-Clapeyron equation. It is:
1/T = -(R)ln[P]/ΔHvap + 1/Tb
Where R = 1.99 cal/K-mole, Tb = 373 K, ΔHvap = 9717 cal/mole.