Most people remember some version of the following three statements as Newton's Laws.
These three laws will be the basis of the next portion of this course. They will be applied in three general situations: (1) Static Equilibrium, (2) Dynamic Equilibrium, and (3) Dynamics (when there is a net force).
In static equilibrium all forces must be balanced. The total forces going up must equal the total forces going down and the total forces going right must equal the total forces going left. We need both of these statements because the vertical and horizontal forces are independent of each other. Also remember that the total forces may be the sum of the components for forces that are not all vertical or horizontal.
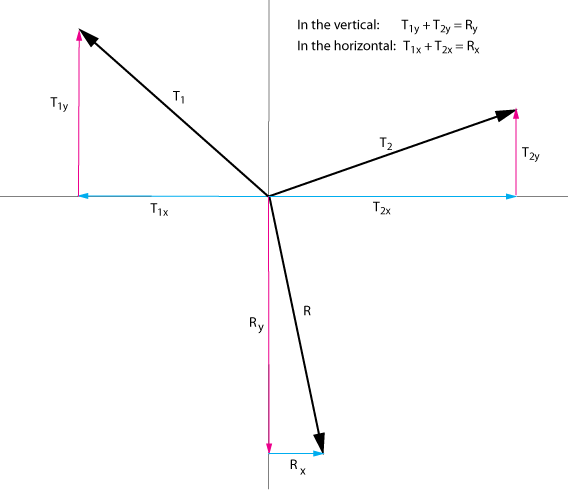
To understand the tension forces T1, T2, and the resultant force R in the graphic we need to apply the idea that up equals down and right equals left. All of the up components added together must equal all of the down components added together and all of the right components added together must add up to all of the left components added together!
In order to actually calculate numbers the following mathematical concepts must be available.
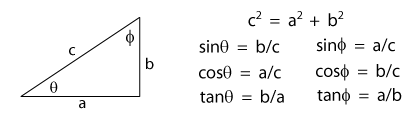
These can also be written as b = (c)(sinθ), a = (c)(cosθ), and c = [a² + b²]½ (remember that an exponent of ½ is the same as a square root). The following graphic shows how this can be used with our force diagram.
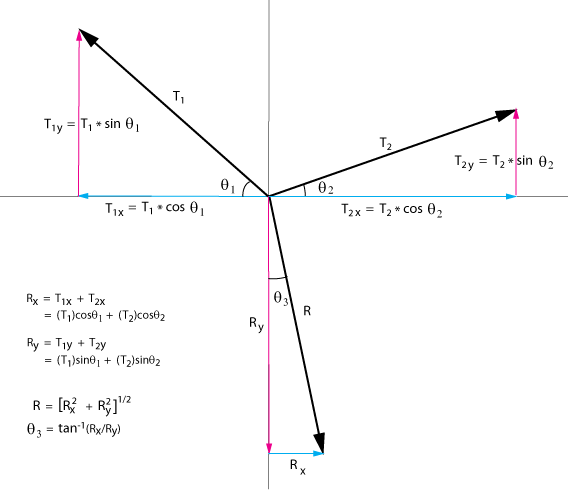
A 25 kg mass is suspended at the end of a horizontal, massless rope that extends from a wall on the left and from the end of a second massless rope connected to a wall on the right at an angle of 130o from the horizontal rope (up 50o from horizontal). What are the tensions in the ropes?
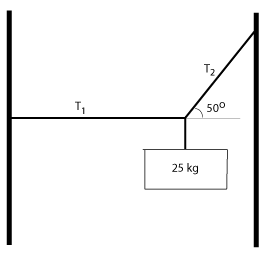
If the axis is chosen such that vertical is the y-axis and horizontal is the x-axis, then only T2 has components in both x and y. For equilibrium to exist, the magnitude of the component of T2 in x, T2x, must equal T1, and T2y must equal the force due to the 25 kg mass, call it F. The magnitude of the force F is the weight of the mass, which is easily found (weight = mg) and equal to T2y. T2x, which is equal to T1, can then be found from T2y using trigonometry concepts. In these equilibrium problems remember that the acceleration due to gravity is always positive and that weight is always directed toward the center of the earth (vertically downward).
F = (25 kg)(9.8 m/sec²) = 245 N = T2y = T2sin50
T2 = 245 N/sin50 = 319.8 N
T1 = T2x = T2cos50 = (319.8 N)cos50 = 205.6 N
In dynamic equilibrium there is no acceleration. The velocity is constant. No acceleration means that all of the forces must be balanced and there isn't any net force available to accelerate the object. It is just like static equilibrium except that the object is moving at a constant velocity. The up still equal the down and the right still equals the left!
A 10 kg block is being pulled up a friction-free ramp with a rope at a constant speed of 1.3 m/sec. The ramp makes an angle of 30o with the horizontal. (a) How much does the ramp push up on the box? (b) What is the tension in the rope?
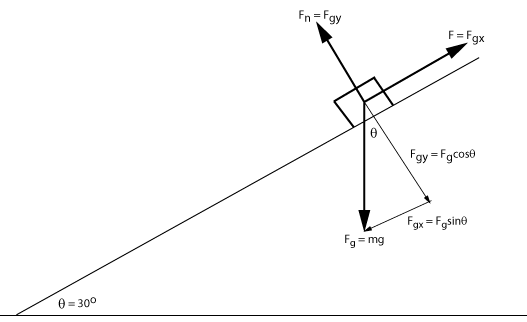
Make the x-axis parallel to the ramp and the y-axis perpendicular to the ramp. That will make the tension in the rope, or the force F, in the positive x-direction. The y-component of F is zero. The normal force Fn, which is how hard the ramp pushes up on the box, only has a y-component in the positive y-direction. The force due to gravity, Fg, will have components in both the x and the y-directions as shown.
Because it is not accelerating we know that all of the forces must balance or the up must equal the down and the right must equal the left. In this case up is perpendicular away from the ramp and right is upward along the ramp.
Vertical: Fn = Fgy = Fgcos30 = (10 kg)(9.8 m/sec²)cos30 = 84.9 N (a) Horizontal: F = Fgx = Fgsin30 = (10 kg)(9.8 m/sec²)sin30 = 49 N (b)
With an acceleration there must be an unbalance or net force that is used to change the velocity. In the last example the force F could be greater than the component of the gravitational force opposing it. If that was the case there would be a net force up the ramp and the block would accelerate upward along the ramp. If we know the forces the acceleration could be calculated using Newton's Second Law, a = netForce/mass. This page will present two examples. The first one will be two masses hanging from a pulley and the second will return to the ramp, but include a frictional force.
A 2 kg mass and a 3 kg mass are hanging from a string that is over a friction-less pulley. (a) What is the acceleration of each mass and (b) what is the tension in the string?
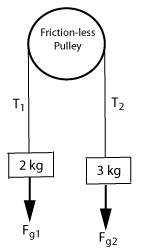
There are two ways to look at these problems. Often one way is easier to start with, and then results from that analysis can be used in the other view to finish the problems. The two ways are (1) Whole system and (2) Isolate masses.
Start with the whole system view. In this pulley system there are really only two forces; the force of gravity on the 2 kg mass and the force of gravity on the 3 kg mass. Because the masses are connected by a string over a pulley, those forces are opposing each other and the system will rotate in the direction of the greater force. In this case the 2 kg mass will go up and the 3 kg mass will go down. In the system view the mass that is moving is the total mass of the system. In this case m = 2 kg + 3 kg = 5 kg.
From this system view and Newton's Second Law (stated as netForce = mass x acceleration) the following equation can be written:
Whole System:
netForce = Fg2 - Fg1
= (3 kg)(9.8 m/sec²) - (2 kg)(9.8 m/sec²)
= 9.8 N = ma
a = (9.8 N)/mass = (9.8 N)/(5 kg) = 1.96 m/sec² (a)
To determine the tension one of the masses must be isolated so that the forces being considered will be the force of gravity pulling down on the mass and the tension pulling up on the mass. The net force is the difference between these two forces on that mass. Notice that T1 and T2 are on the same string and so they must be equal. It also turns out that the acceleration can be determined by isolating both masses and then solving two equations and two unknowns (tension and acceleration). We already have acceleration,so we only need to isolate one of the masses.
Isolate the 3 kg Mass:
netForce = Fg2 - T2 = ma
T2 = Fg2 - ma = (3 kg)(9.8 m/sec²)- (3 kg)(1.96 m/sec²) = 23.52 N (b)
See if you can get the same answer by isolating the 2 kg mass.
Friction depends on how rough the surfaces that are trying to slide on each are and on how hard the surfaces are pushed together. This is reflected in the general equation f = µFn where f is the frictional force, µ is called the coefficient of friction and accounts for the roughness of the surfaces, and Fn is the normal (or perpendicular) force which is the force that one surface is exerting on the other. There are two common kinds of frictional forces, kinetic and static. When one surface is moving along another, the friction is kinetic. If the surface is trying to move, but being stopped by friction it is called static friction. A subscript is used to indicate if it is kinetic or static on both the friction and the coefficient of friction. The equation for kinetic friction would be
fk = µkFn.
A 10 kg block is being pulled with a string parallel to a ramp that makes an angle of 30o with the horizontal. The tension on the string is right at the point where a fraction more tension would cause the box to move up the ramp, but it does remain stationary. The coefficient of static friction between the box and the ramp is 0.13. What is the tension in the string?
Choose the x-axis to be along the ramp and the y-axis to be perpendicular to the ramp. A picture similar to the dynamic equilibrium graphic can be drawn.
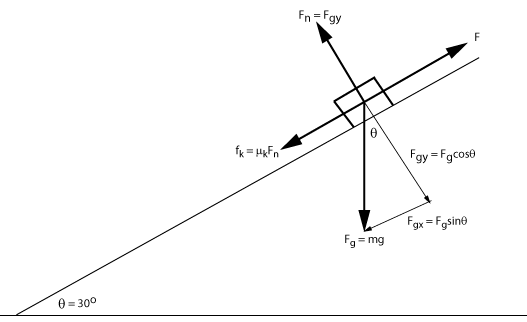
Find the tension for this equilibrium problem and then check your work.
Consider the same block and ramp situation, but with a coefficient of kinetic friction of 0.10. If the string pulls with a force of 80 N, what will the acceleration be?
To get the acceleration we need the net force and mass (a = netForce/mass). The net force is along the ramp and would be the force pulling up the ramp minus the forces pulling the block down the ramp.
netForce = F - fk - Fgx
netForce = 80 N - µkFn - (mg)sin30
netForce = 80 N - (0.10)(mg)cos30 - (mg)sin30
netForce = 80 N - (0.10)(10 kg)(9.8 m/sec²)cos30 - (10 kg)(9.8 m/sec²)sin30]
netForce = 22.5 N
a = netForce/mass = (22.5 N)/(10 kg) = 2.25 m/sec²