The acceleration is the change in velocity with respect to time. Velocity, however, has not only speed, but also direction. If a force changes the speed of an object, the object will accelerate (even if the direction is constant). If a force changes the direction of a moving object the object also accelerates, even if the speed remains constant.
A force that changes the direction of the velocity is called a centripetal force. It is always directed toward the center of the circle of rotation. Friction can act as a centripetal force. A car going around a corner on a flat (unbanked) road doesn't go straight because of the friction between the tires and the road as the wheel is turned. This causes the direction of the motion to change.
We have learned to calculate several kinds of forces: Fg = mg, fs = μsFn, etc. We now introduce another force called the centripetal force. The centripetal force, Fc is equal to the mass times the centripetal acceleration, ac:
Fc = mac
The centripetal acceleration can be given in terms of the angular velocity, ω (rad/sec), the linear velocity, v (m/sec), and the radius, r (m). as shown.
ac = ωv = rω² = v²/r
The centripetal force is due to the tendency of objects to go in straight lines. If an object going in a circular path is "let go", the object would travel at a tangent to the motion. The centripetal force keeps it from going in that straight line and "pulls" it toward the center of the circular motion. When using the centripetal force in calculations, however, it is useful to think of it as the straight line force, or a force that would have the object go away from the center (at a tangent, but away nevertheless). This way of thinking allows us to think about things like the amount of force that friction must exert to keep a car on the road while navigating a turn, for instance.
A car of mass m goes around an unbanked curve at 20 m/sec. If the radius of the curve is 50 m, what is the least coefficient of friction that will allow the car to negotiate the curve without skidding?
In order for the car to not slide, the frictional force must equal the centripetal force:
Fc = fs
mac = μsFn
mv²/r = μsmg
(m)(20 m/sec²)2/(50 m) = μs(m)(9.8 m/sec²)
⇒ μs = 0.82
A section of road that curves with a 95 m radius ices over every winter causing many cars to slide off of the road. How much would the curve need to be banked in order to ensure safe navigation at 13.42 m/sec (30 mi/hr)
For a friction-free curve the gravity pulling the car down the bank has to be countered by the centripetal force. To understand the direction of the centripetal force think about a circular race track. As the car goes around the track at constant speed it will stay at relatively the same height all the way around the track. The center of the circular motion will be in a horizontal plane above the ground at the height of the car. If a rope was holding the car the centripetal force would feel like it pushed opposite the rope (actually in the direction of the tangent) and be directed outward in that same horizontal plane. So, we draw the centripetal force outward parallel to the ground (not parallel to the incline of the banked road). It is, therefore, a component of the centripetal force that opposes the component of gravity which is pulling the car down the incline of the banked road.
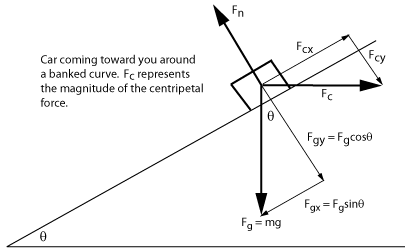
Fgx = Fcx
Fgsinθ = Fccosθ
⇒ tanθ = Fc/Fg = (m)(v²/r)/mg
⇒ θ = tan-1(v²/gr) = 10.9°
A car of mass 2000 kg goes over the crest of a hill whose radius of curvature is 40 m. (a) What is the force of the car on the road's surface at the top of the hill if the car's speed is 15 m/sec? (b) What is the force at the crest if the car is going 20 m/sec? Interpret your answer.
At the top of the hill the gravitational force pulling the car down must at least equal the centripetal force that would make the car go straight (at a tangent to the curve, away from the center). The force of the car on the ground would be the difference between the gravitational force and the centripetal force.
F = Fg - Fc = (2000 kg)(9.8 m/sec²) - (2000 kg)[(15 m/sec)²/(40 m)] = 8350 N
In part (b) the force is -400 N which suggests that there is insufficient weight and the car would become airborne, going at a tangent to the curve, or in this case horizontally.