A vector has both magnitude and direction. Because horizontal and vertical are perpendicular, they are independent of each other and any vector can then be expressed in terms of an x-component and a y-component (x and y are always perpendicular). It is also true that the magnitude and direction of a vector can be determined from its x and y components.
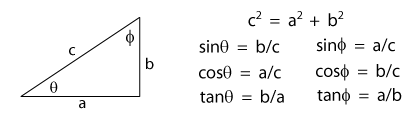
From your math class you should have come across some mathematical expressions for right triangles like the ones shown in the accompanying figure. The top expression is Pythagorean's Theorem and the other expressions are trigonometry functions for right triangles. Be sure to note that these are only good for right triangles (triangles with a 90° angle).
In physics we would say that the side labeled "a" is the x-component, the side labeled "b" is the y-component, and the hypotenuse "c" is the resultant vector. To get the magnitude of the vector we use Pythagorean's theorem and take the square root of the sum of the x-component squared plus the y-component squared.
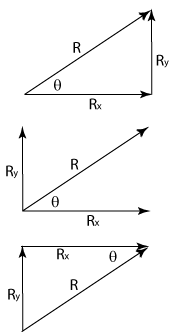
The next figures have labeled the vector R, the x-component Rx, and the y-component Ry. The top figure uses what is called the head-to-tail method of resolving a vector. The end of the vector with the arrowhead is the head and the end without the arrowhead is the tail. In this method we place the head of one component to the tail of the other and then draw the resulting vector from where we started to where we ended. Notice that the bottom of the three figures is also a head-to-tail representation.
As suggested in the figures, it doesn't matter where a vector is drawn as long as the magnitude and direction are not changed. A second way of drawing components is to place them on the x and y-axes as illustrated in the middle figure.
In any case the magnitude of the vector is obtained by the Pythagorean theorem (raising to the ½ is the same as taking the square root):
R = [Rx² + Ry²]½ and θ = tan-1(Ry/Rx)
Also notice that Rx = (R)(cosθ) and Ry = (R)(sinθ)
Sample problem: You walk 4 m, stop, turn 90° and then walk another 3 m. Where will you end up?
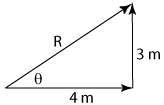
R = [(4 m)² + (3 m)²]½ = 5 m, θ = tan-1(3/4) = 36.9°
You would be 5 m from where you started at an angle of 36.9° from the direction of the 4 m walk (which is on the x-axis).
When adding multiple vectors the general strategy is to determine the x and y components of each of the vectors that are being added, add the x-components together to determine the x-component of the resultant vector (Rx), add the y-components together to determine the y-component of the resultant vector (Ry), and then use Rx and Ry to determine the magnitude and direction of the resultant vector. Can you see how this was done in the sample problem just given?
Example: A vector a, with magnitude a = 6 m at an angle of 30° from the positive x-axis, is add to a vector b, with magnitude b = 4 m at an angle of 40° from the positive x-axis, what is the magnitude and direction of the resultant vector? The first task would be to draw a picture. What would your picture look like? Here are the calculations.
ax = (6 m)(cos30°) = 5.2 m; bx = (4 m)(cos40°) = 3.1 m; Rx = 9.3 m
ay = (6 m)(sin30°) = 3.0 m; by = (4 m)(sin40°) = 2.6 m; Ry = 5.6 m
R = [(9.3 m)² + (5.6 m)²]½ = 10.9 m; θ = tan-1(5.6/9.3) = 31.1°
The resultant vector has a magnitude of 10.9 m at an angle of 31.1° from the positive x-axis.
An alternative way to do the problem would be to first put the x-axis along one of the vectors being added, calculate the angle between the vectors, and then add the vectors together using this method. That way the y-component of one of the vectors would be zero. You might give that a try just for practice.
Note: In case you are still wondering about the sample problem above, here it is using different language. A vector a, with magnitude a = 4 m at an angle of 0°, is added to a vector b, with magnitude 3 m at an angle of 90°. What is the resultant vector?
Use the method illustrated in the previous example and you will see that the y-component of a and the x-component of b are both zero making Rx = ax = a and Ry = by = b.