The current, labeled I, has units of ampere, labeled A, and measures the rate of flow of charge. This will be defined more rigorously later, since it deals with moving charges. The unit for charge, labeled q, is the couloumb, which we label Coul (many books label it C), and it is defined in terms of the the current as follows:
Definition: One coulomb is the quantity of charge carried past a given point in one second by a current of one ampere.
This says that the charge in coulombs is equal to the current in ampere times the time in seconds:
q = It
Example: What is the current of a 100 Coul charge that flows for 10 seconds?
q = It; I = q/t = (100 Coul)/(10 sec) = 10 Coul/sec = 10 A
The charge on one electron is 1.602 x 10-19 Coul.
Example: A current of 5 A flows for 2 sec. How many electrons flow through the wire?
q = It = (5 A)(2 sec) = 10 A-sec = 10 Coul; (10 coul)/(1.602 x 10-19 Coul/electron) = 6.24 x 1019 electrons
Our working model of the atom has a large positive nucleus with much smaller electrons outside of the nucleus. There are two fundamental charged particles, the positive proton and the negative electron. One electron is needed to balance the charge of one proton. If a material has the same number of protons and electrons it is said to be neutral. A charged particle has an uneven number of protons and electrons. If it has extra protons it will have a positive charge. If it has extra electrons it will have a negative charge.
It turns out that the proton has almost 2000 times the mass of an electron. Given that fact, it is easy to understand that if anything is going to move in an atom it will be the electron. The only way to create a charge is to transfer electrons. To get something with a negative charge we transfer electrons to it. To get a positive charge we transfer electrons away from it.
Like charges repel each other and unlike charges attract each other. These repulsive and attractive forces between charges are called Coulombic or electrostatic forces.
What is the relationship between the force (F), the amount of charge on each particle (q1 and q2), and the distance between charges (r)? A general guess is that the force would be directly related to the amount of charge (the greater the charge, the greater the force) and inversely proportional to the distance between the charges (the farther away from each other they are the harder it is to influence each other). Here is some data, can you derive the mathematical relationship?
| q1 (Coul) | q2 (Coul) | r (m) | F (N) |
|---|---|---|---|
| 1 | 1 | 1 | 9 x 109 |
| 2 | 1 | 1 | 18 x 109 |
| 1 | 2 | 1 | 18 x 109 |
| 2 | 2 | 1 | 36 x 109 |
| 1 | 1 | 2 | 2.25 x 109 |
| 1 | 1 | 3 | 1 x 109 |
| 1 | 1 | 4 | 0.5625 x 109 |
The following equation is consistent with the data and is called Coulomb's Law:
F = (k)(q1)(q2)/r²
Where F is the force between the charges, k = 9 x 109 N-m²/Coul², q1 and q2 are the charges on particle one and particle two, and r is the distance between the charges.
What is the distance between a 3.0 Coul and a 4.0 Coul charge that have a force of attraction of 12,000 N?
r = [kq1q2/F]½ = [(9 x 109 N-m²/Coul²)(3 Coul)(4 Coul)/(12,000 N)]½ = 3 x 10³ m
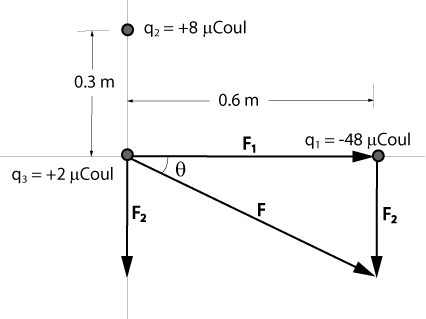
In the x-y plane, a charge of -48 µCoul is on the x-axis at x = 0.6 m, and a charge of +8 µCoul is on the y-axis at y = 0.3 m. Calculate the magnitude and direction of the resultant force on a charge of +2 µCoul that is at the origin.
F1 = (k)(q1)(q3)/r²
= [(9 x 109 N-m²/Coul²)(2 x 10-6 Coul)(48 x 10-6 Coul)]/(0.6 m)²
= 2.4 N
F2 = (k)(q2)(q3)/r²
= [(9 x 109 N-m²/Coul²)(2 x 10-6 Coul)(8 x 10-6 Coul)]/(0.3 m)²
= 1.6 N
F = [F1² + F2²]½
= [(2.4 N)² + (1.6 N)²]½
= 2.88 N
tanθ = (1.6 N)/(2.4 N) = 0.667
θ = 33.7°
Consider a field you are familiar with, the gravitational field. The gravitational field reflects how all masses are always attracted toward the center of the earth. The field could be mapped or drawn by placing small masses at various places around the earth and drawing force arrows that went in the direction of the gravitational pull. In that case all of the arrows would point toward the center of the earth.
The electric field can be drawn the same way, only this time we use a small positive charge to monitor the coulombic force at each point. A collection of the coulombic force arrows is called a vector field, or just field. In this case it is the electric field. The direction of the field is the same as the direction of the force on a small positive test charge, which is designated the unit charge. The strength, or intensity, of the electric field is labeled E, is the coulombic force per unit charge, and has units of N/Coul. E is a vector and is in the same direction as F, the coulombic force on the test charge. If qt is the magnitude of the test charge and k is the coulombic force constant (k = 9 x 109 N-m²/Coul²), the field strength due to charge q is:
E = F/qt = [(k)(q)(qt)/r²]/qt = (k)(q)/r²
Calculate the magnitude and direction of the electric field strength 50 cm directly above a charge of -2 x 10-6 Coul.
E = (k)(q)/r² = (9 x 109 N-m²/Coul²)(-2 x 10-6 Coul)/(0.5 m)² = -7.2 x 104 N/Coul Downward
The negative sign means that the charges have opposite signs, making them attract. Because we are testing a point directly above the charge and it is an attractive force, the force would be directed downward as stated.
This calculation re-enforces the statement that the electric field is the vector field produced by measuring force per unit charge, E = (k)(q)/r².
The potential energy is generally thought of as the amount of work to move an object against a force. The gravitational potential energy is obtained by multiplying the force due to gravity (mg) times the distance moved, given by the height (h): PEgrav = mgh.
The electrical, or electrostatic, potential dfference, V, corresponds to the force needed to move a charge, q, between two points in an electric field. The work is then given by W = Vq.
Example: How much work is required to move an electron between the two terminals of a particle accelerator whose potential difference (PD) is 9 million volts?
W = Vq = (4 x 106 V)(1.6 x 10-19 Coul) = 6.4 x 10-13 V-Coul = 6.4 x 10-13 J
The electric potential has units of volts (V). Two points differ in potential by 1.0 volt if 1.0 Joule of work is required to move 1.0 Coulomb of charge from one point to the other. Note that the unit for work would be volt-Coul and that it must be the same as the energy unit of a Joule.
The electric potential at a point that is a distance, r, from a point charge, q, can be found using the following mathematical model:
V = kq/r
where k = 9 x 109 N-m²/Coul², q is the magnitude of the charge, and r is the distance from the charge. This potential is a scalar and is independent of direction. The unit of potential is the volt, V.
Example: What is the potential at a point 0.1 m from a 10 Coul point charge?
V = (9 x 109 N-m²/Coul²)(10 Coul)/(0.1 m) = 9 x 1011 N-m/Coul = 9 x 1011 J/Coul = 9 x 1011 V
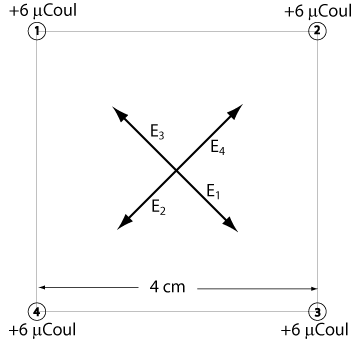
Equal charges of +6 µCoul are positioned at the corners of a square of sides 4 cm long. What are the field and the potential at the center of the square?
Note: These charges each repel a test charge at the center of the square. E3 is directed away from charge number 3 as shown.
All of the electric fields have the same magnitude. E3 is directly opposite E1 and E4 is directly opposite E2. Adding these vectors will result in zero electric field.
The potentials, on the other hand, add as scalars.
V1 = V2 = V3 = V4 = (9 x 109 N-m²/Coul²)(6 x 10-6 Coul)/(2√2 x 10-2) = 1.91 x 106 V
Total Potential = 4(1.91 x 106 V) = 7.64 x 106 V
The capacitance is the ratio of the charge to the potential. The unit of capacitance is the farad, F. A farad is, therefore, a coulomb per volt, as seen in:
C = q/V
A capacitor has two surfaces next to each other, each with the ability to hold a charge. The two surfaces have the same charge, but opposite sign.
Materials placed between the two surfaces of a capacitor are called dielectrics. Different dielectrics have different abilities to change the capacitance of the capacitor. The difference is reflected in the dielectric constant, K. The dielectric constant is the capacitance with a dielectric, Cd, divided by the capacitance in a vacuum, Cvac:
K = Cd/Cvac
The potential energy stored in a capacitor can be expressed in the following ways:
PE = ½qV = ½CV² = ½q²/C
The surfaces of a capacitor are attached to a 6 V battery that produces a charge of 3 Coul. The battery is then disconnected. (a) What is the capacitance of the charged capacitor? (b) The capacitor is submerged in an oil with a dielectric constant of 4.7. What is the new capacitance? (c) What is the potential energy with and without the dielectric?
(a) Cvac = q/V = (3 Coul)/(6 V) = 0.5 F
(b) Cd = KCvac = (4.7)(0.5 F) = 2.35 F
(c) Without the dielectric: PE = ½q²/Cvac = (0.5)(3 Coul)²/(0.5 Coul/V) = 9 Coul-V = 9 J
With the dielectric: PE = ½q²/Cd = (0.5)(3 Coul)²/(2.35 Coul/V) = 1.91 J