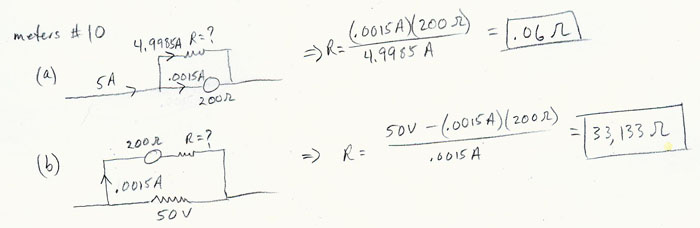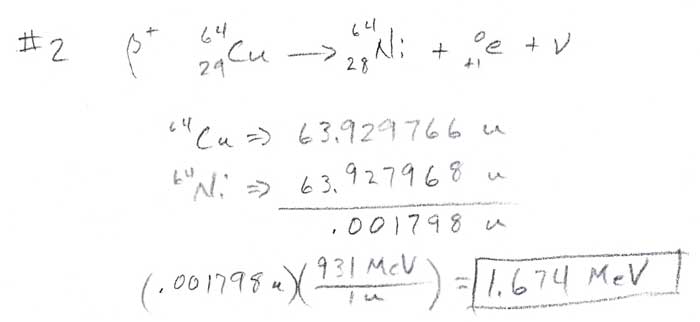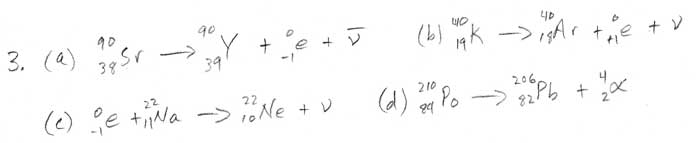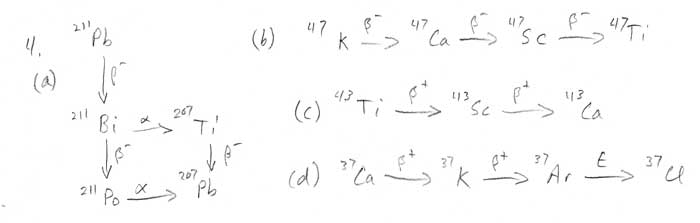Charge and Current
- Answer
- 100 Coul
- Answer
- 0.2 A
- Answer
- 2 sec
Coulomb's Law
- Answer
F = (k)(q1)(q2)/r² = [(9 x 109 N-m²/Coul²)(2 Coul)(3 Coul)]/(0.3 m)²
F = 6 x 1011 N
- Answer
q2 = (F)(r²)/(k)(q1) = (3.5 N)[(1.2 m)²]/[(9 x 109 N-m²)(3.4 Coul)]
q2 = 1.65 x 10-10 Coul
- Answer
q² = (F)(r²)/(k) = (1.2 N)[(0.4 m)²]/(9 x 109 N-m²)
q = 4.62 x 10-6 Coul
- Answer

Electric Field
- Answer
E = (k)(q)/r² = (9 x 109 N-m²/Coul²)(1.8 Coul)/(1.5 m)² = 7.2 x 108 N/Coul
- Answer
E = (k)(q)/r² = (9 x 109 N-m²/Coul²)(-1.8 Coul)/(2.5 m)²
E = -2.59 x 109 N/Coul
- Answer
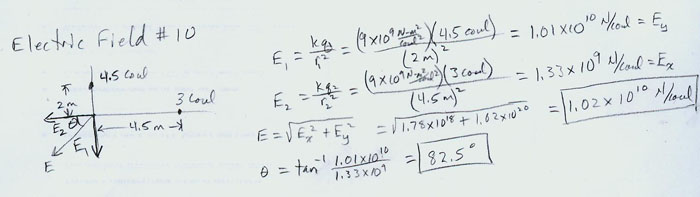
Electric Potential
- Answer
V = (k)(q)/r = (9 x 109 N-m²/Coul²)(1.8 Coul)/(1.5 m)
E = 1.08 x 1010 V
- Answer
V = (k)(q)/r = (9 x 109 N-m²/Coul²)(-1.8 Coul)/(2.5 m)
E = -6.48 x 109 V
- Answer
V = (k)(q)/r; V = V1 + V2
V = (9 x 109 N-m²/Coul²)(3 Coul)/(4.5 m) + (9 x 109 N-m²/Coul²)(4.5 Coul)/(2.5 m)
E = 6 x 109 + 1.6 x 1010 = 2.22 x 1010 V
Electric Field and Electric Potential
- Answer
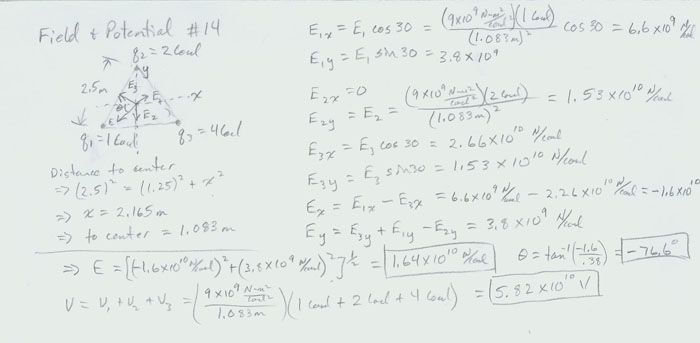
- Answer
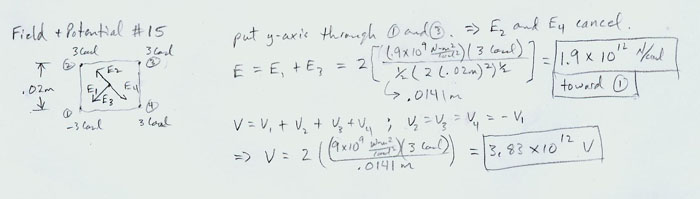
- Answer
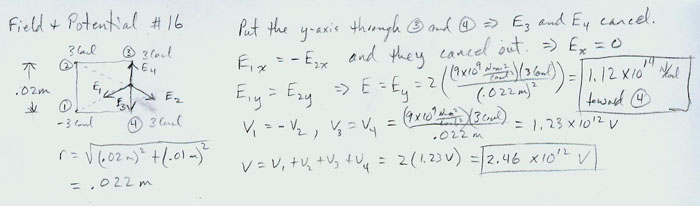
Capacitors
- Answer
q = (C)(V) = (15 x 10-6 F)(1.2 V) = 1.8 x 10-5 Coul