One way for a charge to move is for the charge to spin on an axis. An example is the electron spin. As the electron spins a force field is observed to be formed thatis separate from the electric field produced by the charge on the electron. This new vector field is called the magnetic field (B).
Unpaired electrons can "line up" their spins. In some materials, like iron, these spins can stay lined up in "domains" for a long time and they form "permanent" magnets. The more domains there are the more powerful the magnet is. Other materials, like aluminum, have will line up the electrons when an outside magnetic field is nearby, but when the outside field is taken away the spins return to a random orientation. That is how they pick up and drop cars at the junk yard.
The direction of the magnetic field in a magnet has been assigned away from the "north" and toward the "south". North and south poles don't exist independently. If you cut a magnet in half, there will be two magnets, each with their own north and south poles.
Fmag = I Δl B⊥
Since the current is the charge per time, this expression can be re-written as the charge times the velocity of the charge times the perpendicular B-field:
Fmag = q v B⊥
The direction of Fmag is given by a right hand rule: Point the extended fingers of your right hand in the direction of the velocity (or the change in length) with the palm in the direction of the B-field (the B-field goes out from the palm), the extended thumb will point in the direction of the the magnetic force.
For a small wire segment:
B = (K I Δl)/r²
Where K = 1 x 10-7, I is the current, Δl is the lengthof the wire segment, and r is the distance between the segment and the point where the field is measured.
For an infinitely long straight wire:
B = K(2I)/r
Where K = 1 x 10-7, I is the current, and r is the distance from the wire.
For a circular loop:
B = K(2πI)/r
Where K = 1 x 10-7, π is the number pi, I is the current, and r is the radius of the loop. The direction of the B-field is through the center of the loop (perpendicular to the loop).
Examples
-
A wire carrying 400 A is stretched horizontally in an east-west direction between two towers 60 m apart. The earth's B-field is 45° downward and to the north and the magnitude is 7 x 10-5 N/A-m. What is the magnetic force? If the electrons travel toward the east, what is the direction of the force?
Fmag = I Δl B⊥ = (400 A)(60 m)(7 x 10-5 N/A-m) = 1.68 N
The direction would be 45° downward and to the south (remember conventional current).
-
In a particle accelerator a proton moves horizontally toward the south through a region in which the magnetic induction (the B-field) is 10 T in an upward direction. The proton's speed is 0.1 times the speed of light. Find the magnitude and direction of the force on the proton.
Fmag = qvB⊥ = (1.6 x 10-16 Coul)[(0.1)(3 x 107 N/A-m)](10 T) = 4.8 x 10-11 N
The direction would be horizontal, toward the west (remember conventional current).
-
At an electroplating plant, a long horizontal wire connectiong two buildings carries 500 Atoward the east. What are the magnitude and direction of the magnetic induction (B-field) at a point on the ground 10 m directly below the wire?
B = K(2I)/r = (1 x 10-7 N/A²)(2)(500 A)/(10 m) = 1 x 10-5 T
The direction would be toward the north.
-
Calculate the current in a circular loop 40 cm in radius that would cause a magnetic induction at the center ofthe loop equal to that of the earth's magnetic field, which is about 6 x 10-5 T.
B = K(2πI)/r) = (1 x 10-7 N/A²)(2)(π)(I)/(0.4 m) = 6 x 10-5 T
I = 38.2 A
-
Three long vertical parallel wires are 15 cm apart. The two outer wires have 3 A currents going upward. What is the magnitude and direction of the current in the center wire if all three wires are kept stationary due to the magnetic forces?
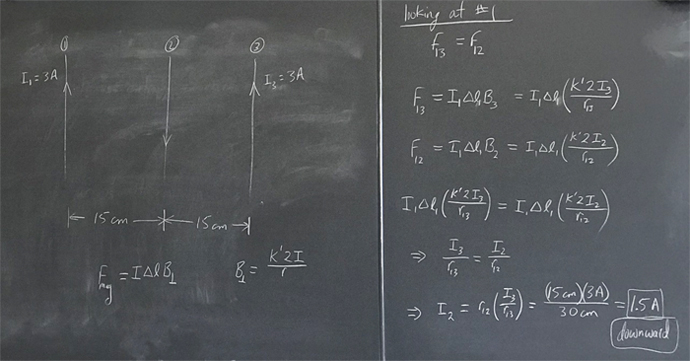
Induced EMF
If a current can produce a magnetic field, it seems logical that a changing magnetic field could produce a current. This changing magnetic field exerts an electromotive force that is responsible for the current. We say that the changing magnetic field produces an induced EMF.
To quantify the induced EMF we define the magnetic flux, Φ, as the magnetic field per unit time. Only the perpendicular component of the B-field will contribute to the magnetic flux. A stronger B-field will produce more magnetic flux and a larger surface area (A) also increases the magnetic flux, as shown in the equation below. The unit of magnetic flux is the weber, Wb.
Φ = B⊥A
The EMF produced in the circuit is given by
E = -ΔΦ/Δt
For a solenoid with N turns
E = -N(ΔΦ)/Δt
Since the perpendicular B-field depends on both the magnitude of B and the angle that the field hits the surface, an EMF can be produced by either changing B (a transformer) or by changing the angle (a generator).
Example
A square loop of wire 4 cm on an edge is lying on a horizontal table. An electromagnet above and to one side of the loop is turned on, causing a uniform magnetic field that is downward at an angle of 30° from the vertical. The magnetic induction is 0.5 T (or 0.5 Wb/m²). Calculate the average induced EMF in the loop if the field increases from zero to its final value in 200 msec.
Φ = B⊥A = (0.5 Wb/m²)(cos30)(4 x 10-2 m)² = 6.93 x 10-4 Wb
E = -ΔΦ/Δt = (6.93 x 10-4 Wb)/(200 x 10-3 sec) = 3.46 x 10-3 V