Light and Optics

Concepts and Definitions

• During reflection light "bounces" off of a surface much like a ball would bounce off of a smooth floor. The path of the light as it goes toward the surface and the path of the light as it goes away from the surface form a plane. In addition the normal (perpendicular) to the reflective surface is also in the same plane. The angle going in (the angle of incidence) is equal to the angle coming out (the angle of reflection). Both the angle of incidence and the angle of reflection are measured from the normal (perpendicular) to the surface.
• Refraction is the bending of light at the interface between two media. Going from air to water would be an example.
  1. As a more dense medium is encountered, the wave is both slowed down and compressed. This means that the speed and the wavelengh will change, but the frequency will remain constant.
  2. In a vacuum the light travels at the "speed of light", c = 3 x 10⁸ m/sec. The speed of the wave in a new medium, v, is related to the speed in a vacuum, c, by a constant called the index of refraction, n: c = nv, or n = c/v.
  3. The angle of refraction is the angle that the ray makes with the normal while in the second medium. The light goes through meduim #1 with index of refraction n₁ toward the surface at an angle from the normal θ₁ and then bends while in medium #2 which has an index of refraction n₂ and an angle from the normal of θ₂ (θ₂ is the angle of refraction).
  4. Snell's Law of Refraction relates medium #1 to medium #2:

     n₁sinθ₁ = n₂sinθ₂

• Light bends toward the normal when it enters an optically denser medium (like air to water). Light bends away from the normal as it enters an optically less dense medium (like water to air).
• At angles higher than the critical angle, θ_c, you get total internal reflection. After the critical angle the light is reflected instead of refracted.

  θ_c = sin^-1(n₂/n₁)

• As light enters a prism it is refracted going into the prism and then refracted again as it comes out of the prism. When the light enters the more dense prism it is bent toward the normal of the first surface. As it leaves the prism it is bent away from the normal of the second surface. This in effect causes the light to bend the same way twice.
• If the base of two prisms are put together the light will be bent downward in the upper half and upward in the lower half, making the two rays cross on the plane where the bases meet. This is like a lens.
• A thin lens is depicted below. Two paths for a ray of light from the top of an object, O, to the bottom of the image, I, (going from A to E) are shown.
• For a thin lens (or thin mirror with appropriate changes) the object distance, p (between H and B), the image distance i (between B and D), and the focal length f (between B and F) are related by the lens equation:
• The magnification is the negative of the image height divided by the object height (-I/O) or, as can be seen by geometry, the negative of the image distance divided by the object distance (-i/p)
• There are conventions for using the lens equation:
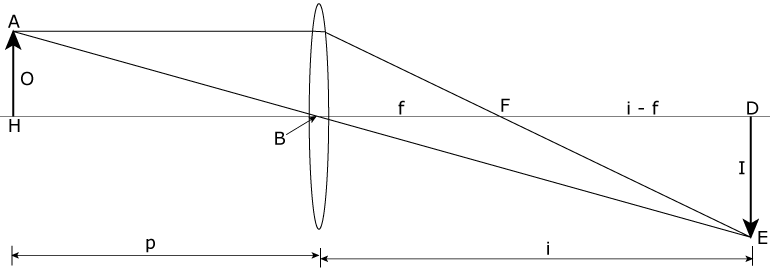
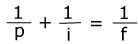
  1. The object distance is always positive if the object is on the side of the lens or mirror from which the light is coming.
  2. The image distance is positive:
     1. In the case of mirrors if the image is on the side of the mirror where the light is, i.e. in front of the mirror.
     2. In the case of lenses if the image is on the side of the lens to which the transmitted light goes.
  3. The focal length of converging mirrors and lenses is positive, while the focal length of diverging mirrors and lenses is negative.
  4. The object distance, p, is always positive, but the image distance, i, is negative for virtual images.

Examples

Snell's Law

A ray of light strikes a piece of glass (n = 1.5), making an angle of 50° with the surface (a) What angle does the refracted ray make with the srrface? (b) What is the speed of the light inside of the glass?

Assume that the index of refraction in air is the same as in a vacuum (n = 1) and remember that the angle of incidence is defined from the normal to the surface. In this case the angle of incidence would be 90° - 50° = 40°

(a) n₁sinθ₁ = n₂sinθ₂; θ₂ = 25° and the angle with the surface is 65°

(b) v₂ = (n₁/n₂)(v₁) = (1/1.5)(3 x 10⁸ m/sec) = 2 x 10⁸ m/sec

The Lens Equation

1. An object 6 mm high is 12 cm to the left of a converging lens of focal length 4 cm. (a) Where is the image? (b) Is it real or virtual? (c) Is it erect or inverted? (d) How large is it?

   (a) 1/12 + 1/i = 1/4; i = 6 cm to the right of the lens

   (b) Because the image is on the opposite side of the lens from the object, the image is real.

   (c) Real images are inverted.

   (d) m = -i/p = -(6 cm)/(12 cm) = - 1/2; the size would be = (0.5)(6 mm) = 3 mm

2. Do the last problem for a diverging lens.

   (a) 1/12 + 1/i = 1/(-4); i = -3 cm to the left of the lens

   (b) Because the image is on the same side of the lens as the object, the image is virtual.

   (c) Virtual images are erect.

   (d) m = -i/p = -(-3 cm)/(12 cm) = 3/12 = 1/4 cm; the size would be = (1/4)(6 mm) = 3/2 mm