No Acceleration
Here is a teaser problem from Click and Clack the Tappet Brothers (Car Talk on NPR).
ROAD TRIP TRIGONOMETRY (week of 8/23/14, Link)
RAY: Last Fall, Tommy and I decided that we were going to take a trip north to see the foliage. Tommy drove the first 40 miles. I drove the rest of the way. We looked at the foliage for three or four minutes, then decided to head home. We took the same route home. On the way back, Tommy drove the first leg of the trip and I drove the last 50 miles. I got home and my wife said, "Who did the driving?" I explained that Tommy drove the first 40 miles, then I drove the rest of the way. On the way back, Tommy drove the first leg of the trip, and I drove the last 50 miles. She said, "But who did most of the driving?" I told her, "You can figure it out. In fact, you can even figure out how much more of the driving was done by that person." And that's the question. Who drove the most -- and how many more miles did that person drive?
Here is another one. I have given you the short version here:
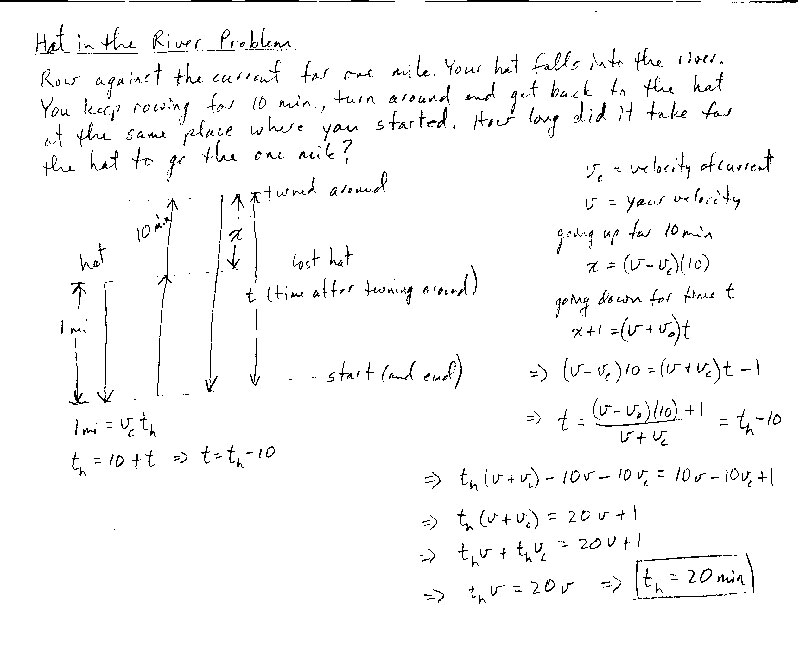
You start rowing a boat against the current and go one mile. Your hat falls into the water at the one mile mark. You continue to row for 10 minutes and then you turn around and row with the current. You catch up with the hat at the same point that you started rowing. How long was the hat floating along in the water?
They provide a nice solution on their website, but here is an
algebraic solution.
Horizontal Acceleration (Friction)
v = 0 m/sec vo = 8.94 m/sec s = ? a = -6.86 m/sec² t = ?
v = vo + at; t = (v - vo)/a = (0 + 8.94 m/sec)/(6.86 m/sec²) = 1.3 sec
v² = vo² + 2as;
s = [v² - vo²]/2a = [0 - (8.94 m/sec)²]/(2)(-6.86 m/sec²) = 5.8 m
- Numerical Answers
- 1.3 sec 5.8 m
v = 0 m/sec vo = ? m/sec s = 30 m a = -3.43 m/sec² t = ?
v² = vo² + 2as;
vo = [v² - 2as]½ = [0 + (2)(3.43 m/sec²)(30 m)]½ = 14.35 m/sec
v = vo + at; t = (v - vo)/a = (0 + 14.35 m/sec)/(3.43 m/sec²) = 4.18 sec
- Numerical Answers
- 14.35 m/sec 4.18 sec
v = 0 m/sec vo = ? m/sec s = ? m a = -4.86 m/sec² t = 2.1 sec
v = vo + at; vo = v - at = 0 + (4.86 m/sec²)(2.1 sec) = 10.2 m/sec
v² = vo² + 2as;
s = [v² - vo²]/2a = [0 - (10.2 m/sec)²]/(2)(-4.86 m/sec²) = 10.7 m
- Numerical Answers
- 10.2 m/sec 10.7 m
Vertical Acceleration (Gravity)
v = -20.0 m/sec vo = ? m/sec s = ? m a = -9.8 m/sec² t = 2.0 sec
vo = v - at = (-20.0 m/sec) + (9.8 m/sec²)(2.0 sec) = -0.4 m/sec
v² = vo² + 2as;
s = [v² - vo²]/2a = [(-20 m/sec)² - (-0.4 m/sec)²]/(2)(-9.8 m/sec²) = -20.4 m
- Numerical Answers
- -0.4 m/sec -20.4 m
From start to max:
v = 0 m/sec vo = ? m/sec s = 10 m a = -9.8 m/sec² t = ? sec
v² = vo² + 2as; vo = [v² - 2as]½ = [0 - (2)(-9.8 m/sec²)(10 m)]½ = 14 m/sec
v = vo + at; t = (v - vo)/a = (0 - 14 m/sec)/(-9.8 m/sec²) = 1.43 sec
Total time is the time to go to max plus the time to come back down:
2(1.43 sec) = 2.86 sec
- Numerical Answers
- 14 m/sec 2.86 sec
v = ? m/sec vo = 0 m/sec s = ? m a = -9.8 m/sec² t = 4.0 sec
s = vot + ½at² = 0 + ½(-9.8 m/sec²)(4 sec)² = -78.4 m
The well is 78.4 m deep.
Also:
v = vo + at = (0 m/sec) - (9.8 m/sec²)(4.0 sec) = -39.2 m/sec
- Numerical Answers
- 78.4 m
1st Time: v = ? m/sec vo = 0 m/sec s = ? m a = -9.8 m/sec² t = 3.0 sec
s = vot + ½at² = 0 + ½(-9.8 m/sec²)(3 sec)² = -44.1 m
2nd Time: v = ? m/sec vo = -3.1 m/sec s = ? m a = -9.8 m/sec² t = 2.7 sec
s = vot + ½at² = (-3.1 m/sec)(2.7 sec) + ½(-9.8 m/sec²)(2.7 sec)² = -44.1 m
Both calculations say the building is 44.1 m high. The model works!
- Numerical Answers
- 44.1 m
v = -50 m/sec vo = 0 m/sec s = ? m a = -9.8 m/sec² t = ? sec
t = (v - vo)/a = [(-50 m/sec) - 0]/(-9.8 m/sec²) = 5.1 sec
s = vot + ½at² = 0 + ½(-9.8 m/sec²)(5.1 sec)² = -127.5 m
It dropped 127.5 m.
- Numerical Answers
- 5.1 sec 127.5 m
Horizontal and Vertical Acceleration (Projectiles)
|
Here are some mathematical relationships that will be helpful for some of these two dimensional problems. | 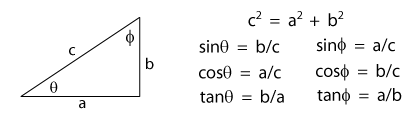
|
Calculate components of the initial velocity in x and y.
In y: voy = vosin25° = (3 m/sec)(sin25°) = 1.27 m/sec
In x: vox = vocos25° = (3 m/sec)(cos25°) = 2.72 m/sec
| y | x | |
| v | ? m/sec | 2.72 m/sec |
| vo | 1.27 m/sec | 2.72 m/sec |
| s | -0.5 m | ? m |
| a | -9.8 m/sec | 0 m/sec |
| t | ? sec | ? sec |
Make a table from jump to water.
Solve for v in the y-direction, then solve for t in the y-direction. Use the time from the y-direction in the x-direction to determine the distance in the x-direction.
vy = [voy² + 2aysy]½ = [(1.27 m/sec)² + (2)(-9.8 m/sec²)(-0.5 m)]½
= -3.38 m/sec
t = (vy - voy)/ay = [(-3.38 m/sec) - 1.27 m/sec]/(-9.8 m/sec²) = 0.474 sec
sx = voxt + ½at² = (2.72 m/sec)(0.474 sec) + 0 = 1.29 m
- Numerical Answers
- 1.29 m 0.474 sec
| y | x | |
| v | ? m/sec | ? m/sec |
| vo | 0 m/sec | ? m/sec |
| s | -1000 m | 2000 m |
| a | -9.8 m/sec | 0 m/sec |
| t | ? sec | ? sec |
Make a table from drop to ground.
Solve for v in the y-direction, then solve for t in the y-direction. Use the time from the y-direction in the x-direction to determine the velocity in the x-direction.
vy = [voy² + 2aysy]½ = [0 + (2)(-9.8 m/sec²)(-1000 m)]½
= -140 m/sec
t = (vy - voy)/ay = [(-140 m/sec) - 0]/(-9.8 m/sec²) = 14.3 sec
vox = sx/t = (2000 m)/(14.3 sec) = 140 m/sec
For the final velocity:
v = [(vx)² + (vy)²]½ = [(-140 m/sec)² + (140 m/sec)²]½ = 198 m/sec
θ = tan-1[(vx)/vy)] = tan-1(140/140) = 45°
v = 198 m/sec at an angle of 45° below horizontal.
- Numerical Answers
- 140 m/sec 198 m/sec at 45° below horizontal.
Get the initial velocity from the initial components.
v0 = [(vox)² + (voy)²]½ = [(160 m/sec)² + (75 m/sec)²]½ = 176.7 m/sec
θ = tan-1[(voy)/vox)] = tan-1(75/160) = 25.1°
The initial velocity is 176.7 m/sec at 25.1° above horizontal.
| y | x | |
| v | 0 m/sec | 160 m/sec |
| vo | 75 m/sec | 160 m/sec |
| s | ? m | ? m |
| a | -9.8 m/sec | 0 m/sec |
| t | ? sec | ? sec |
Make a table going from start to max.
Solve for s in the y-direction to get the maximum height.
sy = [(vy)² - (voy)²)]/[2ay] = [(0 - (75 m/sec)²)]/[2(-9.8 m/sec²)] = 287 m
t = (vy - voy)/ay = [(0 m/sec) - 75 m/sec]/(-9.8 m/sec²) = 7.65 sec (to max)
The total time is 2(7.65 sec) = 15.3 sec
For the distance in x (the range): sx = vot = (160 m/sec)(15.3 sec) = 2449 m
- Numerical Answers
- The initial velocity is 176.7 m/sec at 25.1° above horizontal.
Distance to Max = 287 m, Range = 2449 m
From part (a):
vox = vocosθ m/sec = (17.3 m/sec)cos40° = 13.3 m/sec
voy = vosinθ = (17.3 m/sec)sin40° = 11.12 m/sec
Make a table going from start to max.
| y | x | |
| v | 0 m/sec | vx = vox m/sec |
| vo | 11.12 m/sec | 13.3 m/sec |
| s | ? m | 15 m |
| a | -9.8 m/sec | 0 m/sec |
| t | t sec | t sec |
sy = [(vy)² - (voy)²)]/[2ay] = [(0 - (11.2 m/sec)²)]/[2(-9.8 m/sec²)]
= 6.4 m
t = (vy - voy)/ay = [(0 m/sec) - 11.2 m/sec]/(-9.8 m/sec²) = 1.14 sec (to max)
The total time is 2(1.14 sec) = 2.28 sec
| y | x | |
| v | vsinθ m/sec | vcosθ m/sec |
| vo | vosinθ m/sec | vocosθ m/sec |
| s | 0 m | 30 m |
| a | -9.8 m/sec | 0 m/sec |
| t | t sec | t sec |
Make a table going from start to end.
This will require solving two equations and two unknowns. Solve for t in both the x-direction and the y-direction, then set those expressions equal to each other.
In x: 30 m = (vosinθ m/sec)(t) or t = (30 m)/(vosinθ m/sec)
In y: sy = voyt + ½ayt² = [voy + ½ayt]t
0 = [voy + ½ayt]t says that either t = 0 or [voy + ½ayt] = 0
Time equal to zero is before it starts, so the second expression is needed to agree with the physical situation. So, from y:
t = -voy/½a = -(vosinθ)/½a
That means:
-(vosinθ)/½a = (30 m)/(vosinθ m/sec) or -(vo²)(sinθ)(cosθ) = ½a(30)
vo = -[½a(30)]/[(sinθ)(cosθ)]½ = [(15 m)(9.8 m/sec²)]/[(sin40°)(cos40°)]½
= 17.3 m/sec
- Numerical Answers
- 17.3 m/sec 6.4 m 2.28 sec
Make a table going from start to end.
| y | x | |
| v | vsinθ m/sec | vx = vox m/sec |
| vo | vosinθ m/sec | vocosθ m/sec |
| s | -15 m | 10 m |
| a | -9.8 m/sec | 0 m/sec |
| t | ? sec | ? sec |
Solve for the time in x and substitute the resulting expression into the distance expression for y.
In x: t = (10 m)/(vocos40°)
sy = (voy)t + ½at²
Substiute t from above and then solve for the initial velocity, vo.
-15 m = (vo)(sin40°)[(10 m)/(vocos40°)] + ½(-9.8 m/sec²)[(10 m)/(vocos40°)]²
vo = 5.975 m/sec; voy = 3.84 m/sec; vox = 4.58 m/sec;
t = (10 m)/(4.58 m/sec) = 2.18 sec
vy = 3.84 m/sec - (9.8 m/sec²)(2.18 sec) = -17.52 m/sec
v = [(4.58 m/sec)² + (-17.52 m/sec)²]½ = 18.1 m/sec
θ = tan-1(-17.52/4.58) = 75.3°
- Numerical Answers
- t = 2.18 sec, v = -17.52 m/sec at 75.3° below the positive x-axis.
| y | x | |
| v | 0 m/sec | vx = vox m/sec |
| vo | ? m/sec | ? m/sec |
| s | ? m | ? m |
| a | -9.8 m/sec | 0 m/sec |
| t | 1.05 sec | 1.05 sec |
Symmetry makes this problem much easier.
Make a table going from start to max.
0 = voy + at; voy = -at = (9.8 m/sec²)(1.05 sec) = 10.29 m/sec
vo = (voy)/sinθ = (10.29 m/sec)/sin10° = 59.3 m/sec at 10°
vox = (vo)(cosθ) = (59.3 m/sec)(cos10°) = 58.4 m/sec
Because of the symmetry of this problem the final velocity in y will be the negative of the initial velocity in y. The velocity in x remains constant. θ = tan-1(-10.29/58.4) = -10°
v = [(vx)² + (vy)²]½ = 59.3 m/sec at -10°
sx = (58.4 m/sec)(2.1 sec) = 123 m
- Numerical Answers
- 59.3 m/sec at 10° 59.3 m/sec at -10° 123 m
EXTRA PROBLEMS
- Answer
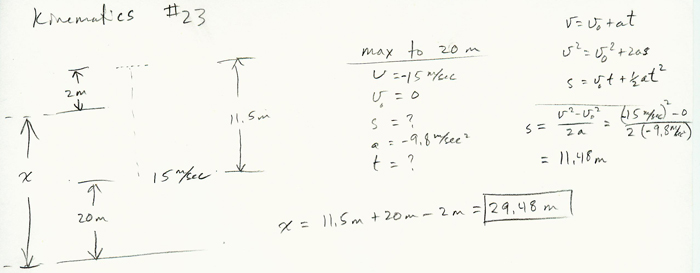
"Your students might immediately want to plug the launch speed and launch angle into the range equation,R is the range, or the distance in x. My questions is: can you derive this equation using our method of doing these problems?R=(v02 sin2θ)/g,
where v0 is the launch speed, g is the acceleration due to gravity, and θ is the vertical launch angle."
- Answer (To see the whole answer, use the link above to the page with visible answers.)